Java en páginas web y hacía sus pininos MathJax, hice unos juguetes. En varias páginas coloqué unas figuras con secantes que se podían mover hacia la tangente, y otras en donde se mostraba cómo disminuye la diferencia entre puntos de la recta tangente y la curva. Ahora los reuní en una página. Espero que lo disfruten.
La secante tiende a la tangente
Cuando desplazamos el punto $B$, sobre la curva, hacia el punto $A$, la secante $\overleftrightarrow{AB}$ se mueve hacia la posición de la tangente a la curva en $A$.
Decimos que cuando $B$ tiende a $A$, la secante $\overleftrightarrow{AB}$ tiende a la tangente a la curva en $A$.
La tangente a la gráfica de una función
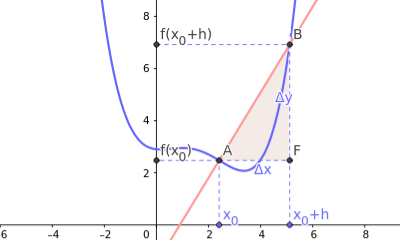
Para hallar la tangente a la gráfica de la función en el punto $\big(x_0, f(x_0)\big)$, trazamos una recta secante que pase, además, por otro punto de la gráfica, el punto $\big(x_0+h, f(x_0+h)\big)$. Al acercar, sobre el eje de las $x$, el punto $x_0+h$ al punto $x_0$, la secante que pasa por los puntos $\big(x_0, f(x_0)\big)$ y $\big(x_0+h, f(x_0+h)\big)$ va colocándose en la posición de la tangente.
La pendiente de la recta secante es $\ m(x_0,h)= \displaystyle\frac{f(x_0+h)-f(x_0)}{h}=\frac{\Delta y}{\Delta x} $.
La pendiente de la recta tangente es el límite de la expresión anterior cuando $h$ tiende a $0$. Le llamamos $f'(x_0)$.
Es decir, la pendiente de la recta tangente a la gráfica $y=f(x)$ en el punto $\big(x_0, f(x_0)\big)$ es: \[ f'(x_0)=\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}=\lim_{h\to0}\frac{f(x_0+h)-f(x_0)}h. \]
La tangente a la curva es la recta que mejor la aproxima, alrededor de $x_0$.
Alrededor de $x_0$ tenemos que $f(x_0+h)$ es $f(x_0)+hf'(x_0)$ más un error que es cada vez más pequeño conforme $h$ tiende a $0$.
El punto $G$ tiene coordenadas $\big(x_0, f'(x_0)\big)$, es decir su ordenada es el valor de la derivada en $x_0$. Al desplazar $x_0$ por el eje de las $x$ veremos el trazo de la función derivada de la función $f$.
La recta tangente y la mejor aproximación lineal.
La ecuación de la recta tangente a $y=f(x)$ en $\big(x_0,f(x_0)\big)$, se obtiene tomando otro punto $(x,y)$ sobre esa recta. Su pendiente, ya vimos, es $f'(x_0)$, y debe ser igual a la diferencia de ordenada entre la diferencia de abscisas, es decir $\displaystyle f'(x_0)=\frac{y-f(x_0)}{x-x_0}$. Despejando $y$ obtenemos la ecuación de la recta tangente $y=f(x_0)+(x-x_0)f'(x_0)$, que la podemos ver en su forma pendiente-ordenada al origen como $y=xf'(x_0)+\big(f(x_0)-x_0f'(x_0)\big)$.
La ordenada al origen nos dice qué tanto hay que desplazar la función lineal $y=xf'(x_0)$ para colocarla en el punto $\big(x_0, f(x_0)\big)$. Es decir, la recta tangente es una recta que pasa por el origen, desplazada hacia el punto en donde es tangente a la curva $y=f(x)$.
